Monday, April 09, 2007

Albert Einstein -- Twin paradox

Twin paradox

From Wikipedia, the free encyclopedia

Jump to: navigation, search

As early as 1905 in his landmark paper on special relativity, On the Electrodynamics of Moving Bodies, Albert Einstein predicted that a clock which is moved away and brought back will lag behind stationary clocks. Einstein called that result "peculiar", but the calculation is straightforward (see section entitled "Specific Example") and the example was not presented as paradoxical. In 1911, Einstein restated this result in the following form:

“ If we placed a living organism in a box ... one could arrange that the organism, after any arbitrary lengthy flight, could be returned to its original spot in a scarcely altered condition, while corresponding organisms which had remained in their original positions had already long since given way to new generations. For the moving organism the lengthy time of the journey was a mere instant, provided the motion took place with approximately the speed of light. (in Resnick and Halliday, 1992) ”

The "twins" entered the discussion in 1911 when Paul Langevin posed a thought experiment in special relativity, where one of two twin brothers undertakes a long space journey with a high-speed rocket at almost the speed of light, while the other twin remains on Earth. When the traveler returns to Earth, he is younger than the twin who stayed put. Langevin explained the different aging of the twins as follows: "Only the traveler has undergone an acceleration that changed the direction of his velocity." According to Langevin, acceleration is here "absolute", in the sense that it is the cause of the asymmetry (and not of the aging itself). Consistent with Einstein, Langevin did not suggest that there was anything paradoxical about it.

Although special relativity predicts differential aging for the traveling twin as compared to the stay-at-home twin, it is not a paradox in the sense of an inherently contradictory result. The perception of paradox, referred to as the twin paradox (sometimes called the 'clock paradox') is caused by the error of assuming that relativity implies that only relative motion between objects should be considered in determining clock rates. The result of this error is the prediction that upon return to Earth, each twin sees the other as younger -- which is clearly impossible.

Contents

[hide]

Specific example

Consider a space ship going from Earth to the nearest star system a distance d = 4.45 light years away, at speed v = 0.866c (i.e., 86.6% of the speed of light). The round trip will take t = 2d / v = 10.28 years in Earth time (i.e. everybody on earth will be 10.28 years older when the ship returns). Ignoring the effects of the earth's rotation on its axis and around the sun (at speeds negligible compared to the speed of light), those on Earth predict the aging of the travellers during their trip as reduced by the factor \epsilon = \sqrt{1 - v^2/c^2}, the inverse of the Lorentz factor. In this case ε = 0.5 and they expect the travellers to be 0.5×10.28 = 5.14 years older when they return.

The ship's crew members calculate how long the trip will take them. They know that the distant star system and the earth are moving relative to the ship at speed v during the trip, and in their rest frame the distance between the earth and the star system is εd = 0.5d = 2.23 light years ("length contraction"), for both the outward and return journeys. Each half of the journey takes 2.23 / v = 2.57 years, and the round trip takes 2×2.57 = 5.14 years. The crew arrives home having aged 5.14 years, just as those on Earth expected.

If a pair of twins were born on the day the ship left, and one went on the journey while the other stayed on earth, the twins will meet again when the traveller is 5.14 years old and the stay-at-home twin is 10.28 years old. This outcome is predicted by Einstein's special theory of relativity. It is a consequence of the experimentally verified phenomenon of time dilation, in which a moving clock is found to experience a reduced amount of proper time as determined by clocks synchronized with a stationary clock. Examples of the experimental evidence can be found at Experimental Confirmation of Time dilation.

Resolution of the paradox in special relativity

The standard textbook approach treats the twin paradox as a straightforward application of special relativity. Here the Earth and the ship are not in a symmetrical relationship: the ship has a "turnaround" in which it feels inertial forces, while the Earth has no such turnaround. Since there is no symmetry, it is not paradoxical if one twin is younger than the other. Nevertheless it is still useful to show that special relativity is self-consistent, and how the calculation is done from the standpoint of the traveling twin.

Special relativity does not claim that all observers are equivalent, only that all observers in inertial reference frames are equivalent. But the space ship jumps frames (accelerates) when it does a U-turn. The twin who stays still, and isn't in a gravitational field (such as say, the earth) rests in the same inertial frame for the whole duration of the flight (no accelerating or decelerating forces apply to him or her) and he is therefore able to distinguish himself as "privileged" compared with the space ship twin. The accepted resolution of the paradox is that a calculation different from that above must be made for the crew, a calculation which explicitly recognizes the change of reference frame, and the change in simultaneity which occurs at the turnaround.

There are indeed not two but three relevant inertial frames: the one in which the stay-at-home twin remains at rest, the one in which the traveling twin is at rest on his outward trip, and the one in which he is at rest on his way home. It is during the acceleration at the U-turn that the traveling twin switches frames. That is when he must adjust the calculated age of the twin at rest.

In special relativity there is no concept of absolute present. A present is defined as a set of events that are simultaneous from the point of view of a given observer. The notion of simultaneity depends on the frame of reference (see relativity of simultaneity), so switching between frames requires an adjustment in the definition of the present. If one imagines a present as a (three-dimensional) simultaneity plane in Minkowski space, then switching frames results in changing the inclination of the plane.

Twins paradox Minkowski diagram
Twins paradox Minkowski diagram

In the spacetime diagram on the right, the first twin's lifeline coincides with the vertical axis (his position is constant in space, moving only in time). On the first leg of the trip, the second twin moves to the right (black sloped line); and on the second leg, back to the left. Blue lines show the planes of simultaneity for the traveling twin during the first leg of the journey; red lines, during the second leg. Just before turnover, the traveling twin calculates the age of the resting twin by measuring the interval along the vertical axis from the origin to the upper blue line. Just after turnover, if he recalculates, he'll measure the interval from the origin to the lower red line. In a sense, during the U-turn the plane of simultaneity jumps from blue to red and very quickly sweeps over a large segment of the lifeline of the resting twin. The resting twin has suddenly "aged" very fast, in the reckoning of the traveling twin.

The twin paradox illustrates a feature of the special relativistic spacetime model, the Minkowski space. The world lines of the inertially moving bodies are the geodesics of Minkowskian spacetime. In Minkowski geometry the world lines of inertially moving bodies maximize the proper time elapsed between two events.

What it looks like: the relativistic Doppler shift

Now, how would each twin observe the other during the trip? Or if each twin always carried a clock indicating his age, what time would each see in the image of the distant twin and his clock? The solution to this observational problem can be found in the relativistic Doppler effect. The frequency of clock-ticks which one sees from a source with rest frequency frest is

f_\mathrm{obs} = f_\mathrm{rest}\sqrt{\left({1 - v/c}\right)/\left({1 + v/c}\right)}

when the source is moving directly away (a reduction in frequency; "red-shifted"). When the source is coming directly back, the observed frequency is higher ("blue-shifted") and given by

f_\mathrm{obs} = f_\mathrm{rest}\sqrt{\left({1 + v/c}\right)/\left({1 - v/c}\right)}

This combines the effects of time dilation (reduction in source frequency due to motion by factor ε) and the Doppler shift in received frequency by factor (1 \pm v/c)-1, which would apply even for velocity-independent clock rates. For the example case above where v / c = 0.866, the high and low frequencies received are 3.732 and 0.268 times the rest frequency. That is each twin would see the image of his sibling aging at a rate 3.732 or 0.268 times his own rate of aging. Note that 3.732 = 1/0.268.

Light paths for images exchanged during tripLeft: Earth to ship. Right: Ship to Earth. Red lines indicate low frequency images are received Blue lines indicate high frequency images are received
Light paths for images exchanged during trip
Left: Earth to ship. Right: Ship to Earth.
Red lines indicate low frequency images are received
Blue lines indicate high frequency images are received

The x − t (space-time) diagrams at left show the path of light signals (carrying the image of the twin and his age-clock) sent between Earth and the Ship during the journey. The vertical black line is the Earth's path through space time and the other two sides of the triangle show the Ship's path through space time (as in the Minkowski diagram above). One diagram shows the signals (carrying images) sent from Earth to Ship, while the other shows the signals sent from Ship to Earth. The images (or signals) are sent at equal intervals in the time of the sender; they are received at unequal intervals in the time of the receiver.

At first each twin would see 1 second pass in the received image of the other twin for every 3.73 seconds of his own time. That is, each would see the image of the other's clock going slow, not just slow by the ε factor, but extra slow because of the Doppler observational effect. This is shown in the figures by red light paths. At some point the images received by each twin change so that each would see 3.73 seconds pass in the image for every second of his own time. That is, the received signal has been increased in frequency by the Doppler shift. These high frequency images are shown in the figures by blue light paths.

The asymmetry in the Doppler shifted images

The asymmetry between the earth and the space ship is manifested in this diagram by the fact that more blue-shifted (fast aging) images are received by the Ship and more red-shifted (slow aging) images are received by Earth. Put another way, the space ship sees the image change from a red-shift (slower aging of the image) to a blue-shift (faster aging of the image) at the mid-point of its trip (at the turnaround, 2.57 years after departure); the Earth sees the image of the ship change from red-shift to blue shift after 9.59 years (almost at the end of the period that the ship is absent). In the next section, you will see another asymmetry in the images: the Earth twin sees the Ship twin age by the same amount in the red and blue shifted images; the Ship twin sees the Earth twin age by different amounts in the red and blue shifted images.

Calculation of elapsed time from the Doppler diagram

The twin on the ship sees low frequency (red) images for 2.57 years. During that time he would see the Earth twin in the image grow older by 2.57/3.73 = 0.69 years. He then sees high frequency (blue) images for the remaining 2.57 years of his trip. During that time, he would see the Earth twin in the image grow older by 2.57×3.73 = 9.59 years. When the journey is finished, the image of the Earth twin has aged by 0.69 + 9.59 = 10.28 years (the Earth twin is 10.28 years old).

The Earth twin sees 9.59 years of slow (red) images of the Ship twin, during which the Ship twin ages (in the image) by 9.58/3.73 = 2.57 years. He then sees fast (blue) images for the remaing 0.69 years until the Ship returns. In the fast images, the Ship twin ages by 0.69×3.73 = 2.57 years. The total aging of the Ship twin in the images received by Earth is 2.57+2.57 = 5.14 years, so the Ship twin returns younger (5.14 years as opposed to 10.28 years on Earth).

The distinction between what they see and what they calculate

To avoid confusion, note the distinction between what each twin sees, and what each would calculate. Each sees an image of his twin which he knows originated at a previous time and which he knows is Doppler shifted. He does not take the elapsed time in the image, as the age of his twin now. And he does not confuse the rate at which the image is aging with the rate at which his twin was aging when the image was transmitted.

  • If he wants to calculate when his twin was the age shown in the image (i.e. how old he himself was then), he has to determine how far away his twin was, when the signal was emitted - in other words, he has to consider simultaneity for a distant event.
  • If he wants to calculate how fast his twin was aging when the image was transmitted he adjusts for the Doppler shift. For example, when he receives high frequency images (showing his twin aging rapidly), with frequency f_\mathrm{rest}\sqrt{\left({1 + v/c}\right)/\left({1 - v/c}\right)}, he does not conclude that the twin was aging that rapidly when the image was generated, any more than he concludes that the siren of an ambulance is emitting the frequency he hears. He knows that the Doppler effect has increased the image frequency by the factor 1/\left(1 - v/c\right). He calculates therefore that his twin was aging at the rate of
f_\mathrm{rest}\sqrt{\left({1 + v/c}\right)/\left({1 - v/c}\right)}\times \left(1 - v/c\right) = f_\mathrm{rest}\sqrt{1 - v^2/c^2}\equiv\epsilon f_\mathrm{rest}

when the image was emitted. A similar calculation reveals that his twin was aging at the same reduced rate of εfrest in all low frequency images.

Simultaneity in the Doppler shift calculation

It may be difficult to see where simultaneity came into the Doppler shift calculation, and indeed the calculation is often preferred because one does not have to worry about simultaneity. As seen above, the Ship twin can convert his received Doppler-shifted rate to a slower rate of the clock of the distant clock for both red and blue images. If he ignores simultaneity he might say his twin was aging at the reduced rate throughout the journey and therefore should be younger than him. He is now back to square one, and has to take into account the change in his notion of simultaneity at the turn around. The rate he can calculate for the image (corrected for Doppler effect) is the rate of the Earth twin's clock at the moment it was sent, not at the moment it was received. Since he receives an unequal number of red and blue shifted images he should realise that the red and blue shifted emissions were not emitted over equal time periods for the Earth twin, and therefore he must account for simultaneity at a distance.

Resolution of the paradox in general relativity

The issue in the general relativity solution is how the traveling twin perceives the situation during the acceleration for the turn-around. This issue is well described in Einstein's twin paradox solution of 1918[1]. In this solution it was noted that from the viewpoint of the traveller, the calculation for each separate leg equals that of special relativity, in which the Earth clocks age less than the traveller. For example, if the Earth clocks age 1 day less on each leg, the amount that the Earth clocks will lag behind due to speed alone amounts to 2 days. Now the accelerated frame is regarded as truly stationary, and the physical description of what happens at turn-around has to produce a contrary effect of double that amount: 4 days' advancing of the Earth clocks. Then the traveller's clock will end up with a 2-day delay on the Earth clocks, just as special relativity stipulates.

The mechanism for the advancing of the stay-at-home twin's clock is gravitational time dilation. When an observer finds that inertially moving objects are being accelerated with respect to themselves, those objects are in a gravitational field in so far as relativity is concerned. For the traveling twin at turn-around, this gravitational field fills the universe. (It should be emphasized that this gravitational field is only perceptual as it is caused by the traveling twin's acceleration, but its effect on how the stay-at-home twin is perceived is quite real.) In a gravitational field, clocks tick at a rate of t' = t(1 + Φ / c2) where Φ is the gravitational potential. In this case, Φ = gh where g is the acceleration of the traveling observer during turnaround and h is the distance to the stay-at-home twin. h is a positive value in this case since the rocket is firing towards the stay-at-home twin thereby placing that twin at a higher gravitational potential. Due to the large distance between the twins, the stay-at-home twin's clocks will appear to be sped up enough to account for the difference in proper times experienced by the twins. It is no accident that this speed-up is enough to account for the simultaneity shift described above.

It should be noted that although this is called a "general relativity" solution, it in fact is done using findings related to special relativity for accelerated observers that Einstein described as early as 1907 (namely the equivalence principle and gravitational time dilation). So it could be called the "accelerated observer viewpoint" instead. It has been recently shown that the general relativity solution for a static homogeneous gravitational field and the special relativity solution for finite acceleration produce identical results.[2]

Accelerated rocket calculation

Let clock K be associated with the "stay at home twin". Let clock K' be associated with the rocket that makes the trip. At the departure event both clocks are set to 0.

Phase 1: Rocket (with clock K') embarks with constant proper acceleration a during a time A as measured by clock K until it reaches some velocity v.
Phase 2: Rocket keeps coasting at velocity v during some time T according to clock K.
Phase 3: Rocket fires its engines in the opposite direction of K during a time A according to clock K until it is at rest with respect to clock K. The constant proper acceleration has the value -a, in other words the rocket is decelerating.
Phase 4: Rocket keeps firing its engines in the opposite direction of K, during the same time A according to clock K, until K' regains the same speed v with respect to K, but now towards K (with velocity -v).
Phase 5: Rocket keeps coasting towards K at speed v during the same time T according to clock K.
Phase 6: Rocket again fires its engines in the direction of K, so it decelerates with a constant proper acceleration a during a time A, still according to clock K, until both clocks reunite.

Knowing that the clock K remains inertial (stationary), the total accumulated proper time Δt' of clock K' will be given by the integral

\Delta t' = \int \sqrt{ 1 - (v(t)/c)^2 }dt \

where v(t) is the velocity of clock K' as a function of t according to clock K.

This integral can be calculated for the 6 phases:

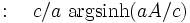
Phase 1 :\quad c / a \ \text{argsinh}( a A/c )\,
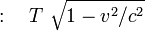
Phase 2 :\quad T \ \sqrt{ 1 - v^2/c^2 }
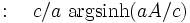
Phase 3 :\quad c / a \ \text{argsinh}( a A/c )\,
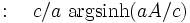
Phase 4 :\quad c / a \ \text{argsinh}( a A/c )\,
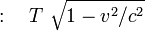
Phase 5 :\quad T \ \sqrt{ 1 - v^2/c^2 }
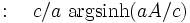
Phase 6 :\quad c / a \ \text{argsinh}( a A/c )\,

where a is the proper acceleration, felt by clock K' during the acceleration phase(s) and where the following relations hold between v, a and A:

v = a A / \sqrt{ 1 + (a A/c)^2 }
a A = v / \sqrt{ 1 - v^2/c^2 }

So the travelling clock K' will show an elapsed time of

\Delta t' = 2 T \sqrt{ 1 - v^2/c^2 } + 4 c / a \ \text{argsinh}( a A/c )

which can be expressed as

\Delta t' = 2 T / \sqrt{ 1 + (aA/c)^2 } + 4 c / a \ \text{argsinh}( a A/c )

whereas the stationary clock K shows an elapsed time of

\Delta t = 2 T + 4 A\,

which is, for every possible value of a, A, T and v, larger than the reading of clock K':

\Delta t'\,">

Notes

  1. ^ Einstein, A. (1918) "Dialog über Einwände gegen die Relativitätstheorie", Die Naturwissenschaften 48, pp697-702, 29 November 1918 (English translation: dialog about objections against the theory of relativity)
  2. ^ Jones, Preston; Wanex, L.F. (February 2006). "The clock paradox in a static homogeneous gravitational field". Foundations of Physics Letters 19 (1): 75–85.

See also

References

Wikibooks
Wikibooks has a book on the topic of

External links

Posted by Its not my name at 8:26 AM

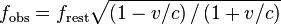
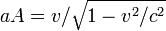
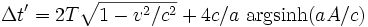
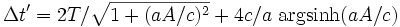
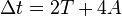
No comments:

Post a Comment

Subscribe to: Post Comments (Atom)